
Degenerate Modes
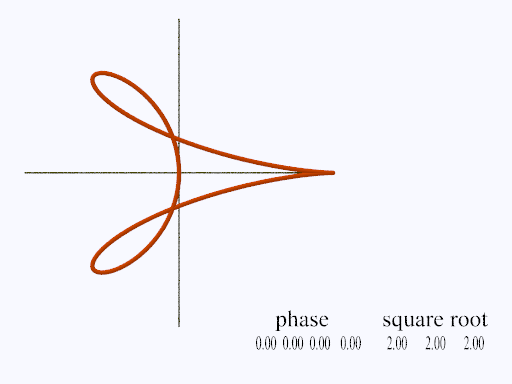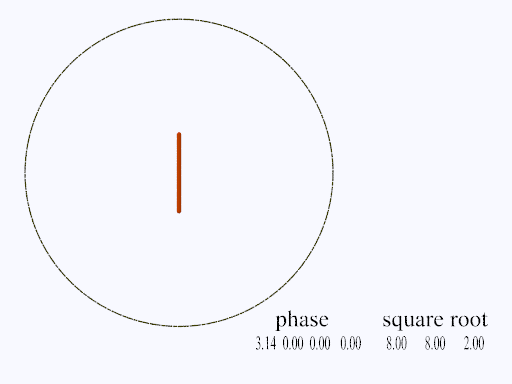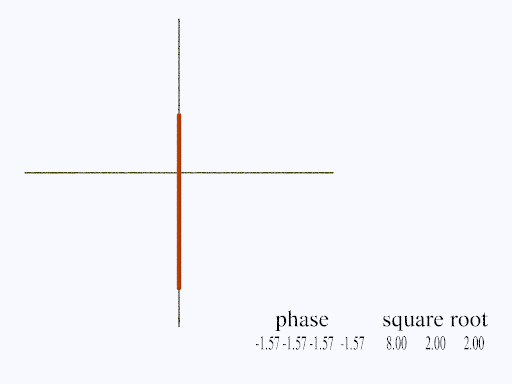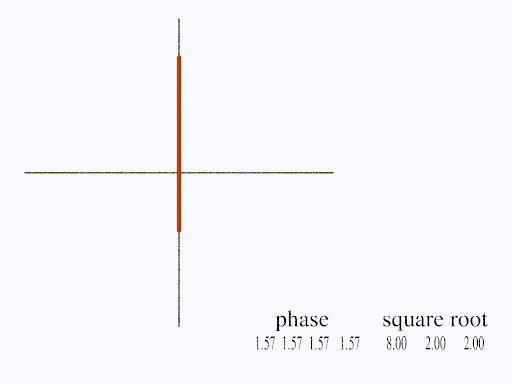
Stingray Lissajous Figure

Computer generated music, RAD
A difference equation might suggest small increments; these steps actually increase by whole numbers;
tn = tn + pi / (0.5 + sqrt(2)),
which means n times tn.
For a Lissajous Figure to be coherent, it must be commensurate. This pair of equations looks suspicious.
xn = cos(tn) + cos(sqrt(2) * tn)
yn = c * sin(tn) + sin(sqrt(2) * tn)
tn = tn + pi / (c + sqrt(2))
If c = 0.5 we have Stingray trajectory. If c = 1, then two straight lines cross on the x-y axes, as you can see in the diagram. The lines, of closely spaced dots, will be less than or equal to the absolute value of two.
It is easy enough to show that the cross consists of dots only on the x-y axes; in other words, xn and yn are alternately zero. Since
cos A + cos B = 2 cos (A+B)/2 * cos(A-B)/2
we have, cos(A + B) = pi * n / 2 = 0 for odd numbered n and for
sin A + sin B = 2 sin(A + B)/2 * cos(A + B)/2
we have 1 for odd numbered n.
For the first few terms: n, xn , yn we have:
1 0.00 1.93
2 -1.72 0.00
3 0.00 -1.38
4 0.95 0.00
5 0.00 0.44
Parametric, difference equation in polar coordinates
#include “colors.inc”
light_source {
0*x
color rgb <1,1,1>
translate <-20, 40, -20>
}
background { color rgb<.94, .95, 1> }
camera { orthographic
location <0, 0, -6>
look_at <0, 0, -1>
}
#declare xn = 0;
#declare yn = 0;
#declare tn = 0;
#declare a1 = pi;
#declare a2 = 0;
#declare b1 = pi;
#declare b2 = 0;
#declare c = 0.5;
#declare I = 0;
#while(I <= 1777)
#declare xn = cos(tn + a1 ) + cos(sqrt(2) *tn + a2);
#declare yn = c* sin(tn +b1) + sin(sqrt(2)*tn+b2 );
#declare tn = tn + pi/ (c +sqrt(2)) ;
sphere { <0,0,0>, 0.015
texture { pigment{ color rgb< 0.5, 0.05, 0.00>}
finish { ambient .7}
} // end of texture
scale<1,1,1> rotate<0,0,0> translate<xn,yn, 0>
}
#declare I = I + 1;
#end
#declare xn = 0;
#declare yn = 0;
#declare tn = 0;
#declare a1 = 0;
#declare b1 = 0;
#declare c = 1.0000;
#declare I = 0;
#while(I <= 1777)
#declare xn = cos(tn + a1 ) + cos(sqrt(2) *tn + a2);
#declare yn = c* sin(tn +b1) + sin(sqrt(2)*tn+b2 );
#declare tn = tn + pi/ (c +sqrt(2)) ;
sphere { <0,0,0>, 0.01
texture { pigment{ color rgb< 0.05, 0.05, 0>}
finish { ambient .7}
} // end of texture
scale<1,1,1> rotate<0,0,0> translate<xn,yn, 0>
}
#declare I = I + 1;
#end

